Research Interests
I work in the field of theoretical condensed matter physics and quantum information. I am interested in a diverse range of quantum phenomena, such as many-body entanglement, many-body localization, measurement-induced phase transitions, topological matter, tensor networks, and classical shadow tomography. All of my work utilizes a mix of theoretical and numerical tools.

- Many-body entanglement dynamics
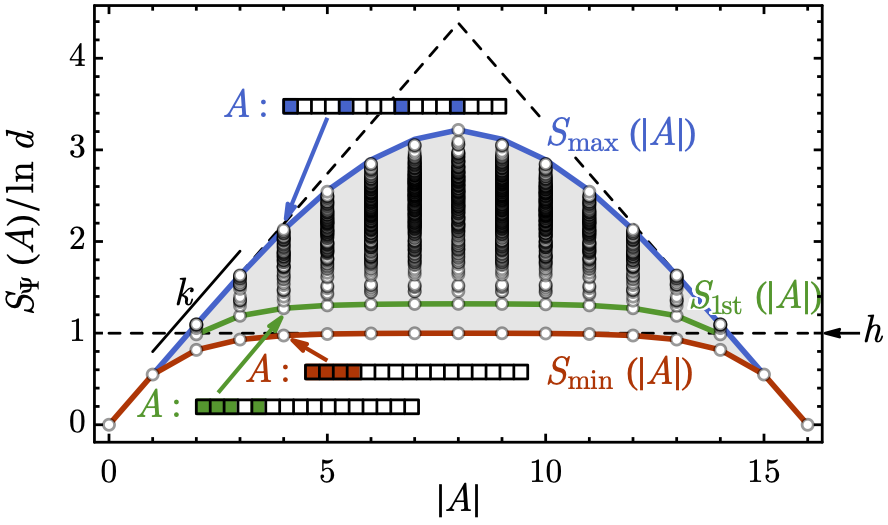
Entanglement quantifies how quantum information spreads over space and time. Whether quantum matter obeys an entanglement area-law or entanglement volume-law can reveal much about its phase, topology, error-correcting capacity, etc. However, the curse of dimensionality means that there is a lot of entanglement data: one for each bipartition of a system.
In [1,2], we have studied a class of random quantum circuits which erase local basis information. We found that these ubiquitous models are amenable to analytical and numerical treatment because they admit a Markovian description. This allowed us to discover a correction to contiguous-region entanglement dynamics from disconnected regions that were missing from previous coarse-grained analyses. Furthermore, we found that the entire entanglement spectrum, i.e. entanglement for all possible bipartitions arranged according to region size, is captured by just two parameters: the cost of creating an entanglement domain wall and the slope of entanglement with sub-system size. This insight provided numerical and analytical tools to study quantum information dynamics in random circuits. What other models of “exactly-solvable” entanglement dynamics are there and what can we learn from them?
In past works, we developed a notion of an entanglement-features Hamiltonian, which defines an imaginary-time Schrodinger equation for the entanglement data itself. However, entanglement dynamics only characterizes one aspect of quantum complexity–the other is magic, which characterizes the “stabilizerness” of a quantum state. Is there a magic-features Hamiltonian, and what can it tell us about quantum complexity and chaos? We know that quantum chaos is inherently magical [3]. Moreover, recent works have developed one way to quantify magic called CSS entropywhich was used to study magic dynamics in a brick-wall random circuit, suggesting that a magic-features Hamiltonian may not be so inconceivable [4]. Furthermore, a magic-features Hamiltonian could shed light on how a single, non-Clifford gate can drive transitions in sampling outcomes or shift the entire entanglement spectrum [5,6]. The simplicity of these circuit models implies that they may also have tractable entanglement dynamics, providing a playground to study magic and entanglement dynamics simultaneously.
|
Entanglement for all Possible Bipartitions, Sorted by Partition Size |
|
|
|
Caption: Entanglement data for typical states has an interesting structure to it. The minimal entanglement is for contiguous regions, depicted in red. The contiguous bipartition acts as a kind of gapped ground state, separating a continuum of excited states formed by adding domain walls while keeping the size of the bipartition fixed. The gap, along with the “cost” of increasing the size of the bipartition, fully characterize the entanglement “spectrum.” |
- Classical Shadow Tomography
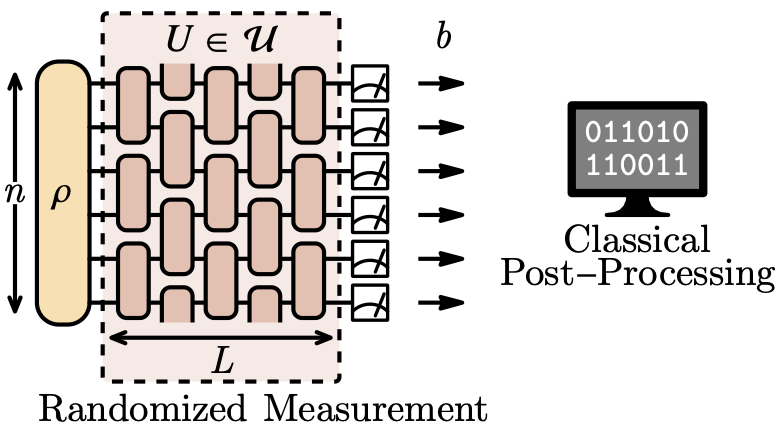
Classical shadow tomography is an efficient protocol for predicting properties of quantum states. Due to its simplicity, it has direct applicability on existing quantum devices. Traditionally, the literature has focused on two tomography schemes: Pauli measurements, which are useful for predicting low-weight operators, and Clifford measurements, which are useful for predicting low-rank operators. The two schemes correspond to the t=0 and t=∞ limits of a brick-wall circuit composed of Clifford gates. In [10,11], we demonstrated an efficient technique for performing classical shadow tomography in the shallow circuit regime inspired by tensor networks. We found that these intermediate schemes can be useful for predicting quasi-local operators, as well as estimating fidelity without having to apply global Clifford gates, which can be difficult to implement in current devices.
|
Using Shallow Quantum Circuits for Classical Shadow Tomography |
|
Caption: Classical Shadow Tomography is a powerful, yet deceptively simple, scheme for learning properties of a quantum state. It consists of three steps repeated over and over: apply a random unitary from a fixed ensemble, measure all the qubits, (classically) record the measurement outcome and the specific unitary which was applied. If we choose the unitary ensemble wisely, we can optimize for predicting different types of operators. In shallow-circuit tomography, the choice of ensemble is a brick-wall circuit composed of random two-local Clifford rotations. By interpolating between locally and globally scrambling regimes, shallow circuit tomography is good at predicting a wide range of operators. |
|
|
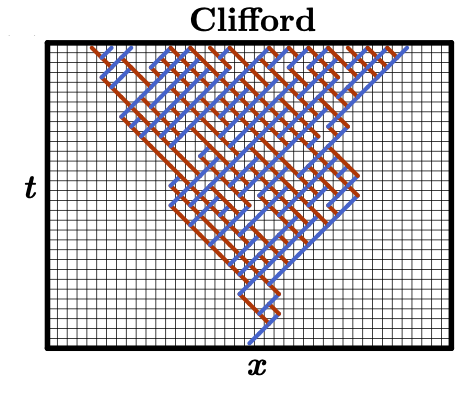
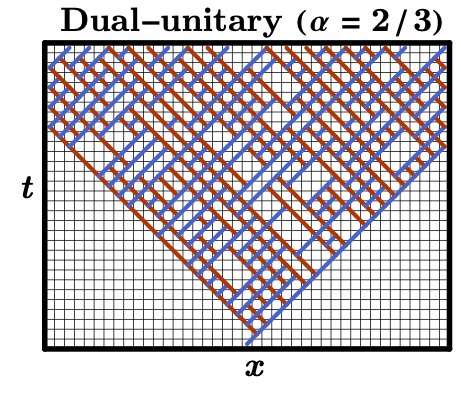
We also studied finite-depth circuits composed of dual-unitary gates, rather than Clifford gates, in classical shadow tomography. It is well known that dual-unitary gates are good at scrambling quantum information, and have found use in many exotic areas of physics such as modeling black hole phenomena. In our work, we show that the fast-scrambling nature of dual-unitary gates allows them to more quickly approach the Clifford measurement t=∞ limit than brick-wall Clifford circuits.
We also find that the operator spreading dynamics in such circuits exhibit rich physics, including light-cones and chiral excitations. Since quantum phases can broadly be characterized by states related by some sequence of local (unitary or non-unitary) operations, and such operations can similarly define a classical shadow scheme, I would like to explore what insights into the theory of quantum phases of matter can be gleaned from this practical framework. Dual-unitary circuits also provide an exactly solvable “minimal model” for quantum chaos. What can we learn about optimal shadow tomography for other exactly solvable models such as free fermions (matchgates), free bosons (linear optics), SYK models, etc.?
|
|
|
|
Caption: The dynamics of the weight of an operator under a brick-wall quantum circuit are very different depending on whether we use Clifford or Dual-Unitary gates. The figures above depict the support of an initially localized observable as it evolves under a brick-wall circuit composed of Clifford gates (left) or Dual-Unitary gates (right). At each step, the weight can move, branch, or fuse with neighboring weights. In the Dual-Unitary setting, the weight has an inherent chirality, so that it will continue to propagate in a given direction until it’s fused or hits a boundary. Within the light-cone, the operator is rapidly scrambled. The competition between ballistic spreading of the Pauli weight and scrambling within the bulk results in logarithmic scaling of the optimal circuit depth with the operator size. |
|
More generally, I am interested in how classical shadow tomography can be used to diagnose quantum complexity. One characterization of complexity that arises naturally in classical shadow tomography is the shadow norm, which specifies how hard it is to predict an operator given a particular classical shadow tomography scheme. The shadow norm adds nuance to the traditional notions of quantum complexity, as the “complexity” is now relative to an operator and a particular kind of dynamics. How does this shadow norm relate to other measures of quantum complexity or quantum information dynamics?
The dynamics of quantum systems are still being explored, for example, in notions of chaos and scrambling. Previous works have shown that chaos is not simply scrambling e.g. even integrable systems with unstable fixed points can be strong scramblers [12,13]. Can the shadow norm distinguish between these two concepts? Little is known about the effectiveness of classical shadow protocols outside of a handful of solvable examples. In classical shadow tomography, the rich interplay between state, hamiltonian, and observable is still largely unknown. The existence of a kind of general “glossary” in classical shadow tomography, where one inputs a state, a hamiltonian, and an operator, and gets a shadow norm as output, would be useful on a numerical and theoretical level.
- Dynamical Phase Transitions
Disorder can localize particles through destructive interference and scattering. Whether such localization can persist in the presence of interactions and allow a quantum system to evade thermalization is the central question in many-body localization. These are a kind of dynamical phase transition which is in part characterized by a transition in the scaling of the many-body entanglement. Another such example is the measurement-induced phase transitions, where one tunes the measurement rate p to drive an entanglement transition.
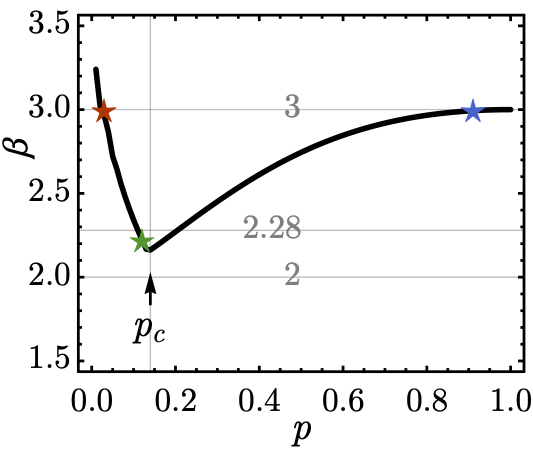
In [7,8], we have studied localization in the low-lying states of the massless Schwinger model through a variety of numerical techniques including simulation using matrix product states and exact diagonalization to study eigenvalue statistics. More recently, we revisited the measurement-induced phase transition when viewed as a classical shadow tomography prediction scheme. We found that the optimal scaling of the sample complexity 𝛃 is obtained at precisely the critical point separating the area and volume-law phases. There are several unfinished questions I would like to explore here: what is the nature of the critical point? How does it change when we incorporate symmetries? Will other dynamical transitions exhibit tomographic optimality, such as disorder-induced localization transitions?
Recent works in measurement-induced criticality have incorporated how symmetry can modify the transition [9]. In the case of a U(1) symmetry, researchers found that the volume law phase splits into a charge-fuzzy and charge-sharp phase, depending on whether the measurements effectively collapse charge fluctuations. In the charge-sharp phase, an neutral observer can learn the total amount of charge in a subregion, whereas in the charge-fuzzy phase they cannot. How does this learnability transition manifest in the structure of the measurement channel of the corresponding classical shadow tomography scheme? How is the optimality parameter 𝛃 modified in the presence of symmetries?
|
|
Caption: Suppose we could do classical shadow tomography using intermittent measurements, performed with probability p, with the goal of predicting observables with arbitrarily large support. We can characterize our efficacy at prediction by 𝛃, which tells us how the number of runs one has to do to reliably predict an operator scales with the spatial extent of the operator. We find that this quantity 𝛃 is minimized at measurement induced criticality. In the area-law phase, this is because reducing the rate of measurements models shallow-circuit tomography. In the volume-law phase, this is because quantum information can evade successfully capture from infrequent measurements. |
References:
- Kuo, Akhtar, You and Arovas. (2020). Markovian entanglement dynamics under locally scrambled quantum evolution. PRB.
- Akhtar and You. (2020). Multiregion entanglement in locally scrambled quantum dynamics. PRB.
- Leone, Oliviero, Zhou and Hamma. (2021). Quantum Chaos is Quantum. arXiv.
- Turkeshi, Tirrito, and Sierant. (2024). Magic spreading in random quantum circuits. arXiv.
- Hinsche et. al. (2022). A single T-gate makes distribution learning hard. arXiv.
- Zhou, Yang, Hamma, Chamon. (2020). Single T gate in a Clifford circuit drives transition to universal entanglement spectrum statistics. arXiv.
- Akhtar, Nandkishore, and Sondhi. (2018). Symmetry breaking and localization in a random Schwinger model with commensuration. PRB.
- Akhtar, Hu, and You. (2024). Measurement-induced criticality is tomographically optimal. PRB.
- Barratt et. al. (2022). Transitions in the learnability of global charges from local measurements. arXiv.
- Akhtar, Hu and You. (2023). Scalable and Flexible Classical Shadow Tomography with Tensor Networks. Quantum.
- Akhtar, Anand, Marshall and You. (2024). Dual-Unitary Classical Shadow Tomography. arXiv.
- Xu, Scaffidi, and Cao. (2019). Does scrambling equal chaos? arXiv.
- Dowling, Kos and Modi. (2023). Scrambling is Necessary but Not Sufficient for Chaos. arXiv.